To build off my last blog about addition and subtraction, I would like to look at different strategies and models used in multiplication and division. It’s very important that students have an understanding of what they are doing — and not just memorize steps and procedures. They need to be able to analyze and think critically about numbers and how they are related. The traditional multiplication and division algorithms are important and every student does need to know how to use them, but not until after they have solidified their understanding. Starting with a concrete concept, moving to the pictorial and finally ending with the abstract will help students develop fully mastery.
Below are some models that students are using to help them understand the relationship between multiplication and division. Hopefully seeing these models and understanding how to use them will help you when you see your child using them.
Arrays: These are one of the earliest models used to help understand the concept of multiplication and division. They help students see the connection between the two operations, and students can visually see the “grouping” or “sharing” concept. Arrays are a great way to help students memorize their multiplication and division facts, instead of just using flash cards.
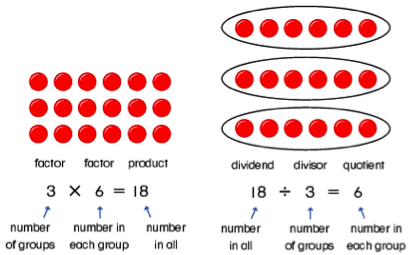
Image: Eduplace.org
Area Models: The area model is closely related to the computation used when computing with the standard algorithm. The difference is the visual representation and connection to the Base 10 System, and the understanding of place value. Students can visually see the actual size of each computation and learn how to interpret the partial products.
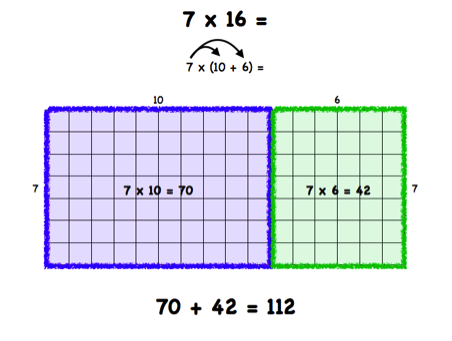
Image: Tes.com
Bar Models: Bar models are based on the concept of equal groups and part-part-wholes. This model helps students in moving away from the concrete phase and begins to help them understand the pictorial stage. Bar models are a great way to help students show their thinking when problem solving, especially when solving two-step problems.
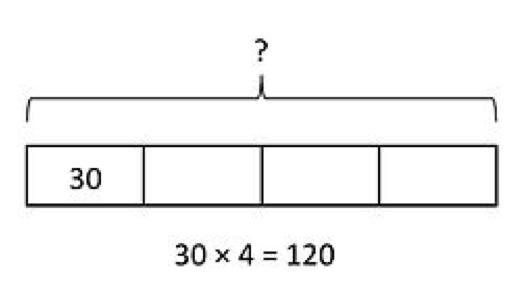
Image: Wikipedia.org
Number Lines: Number lines allow students to begin understanding the abstract stage of multiplication and division. Students begin to connect skip counting and multiples of a number to finding the product of a factor. They can “skip” forwards or backwards to represent the inverse operation. Number lines are great models to help students show their thinking and explain their reasoning.
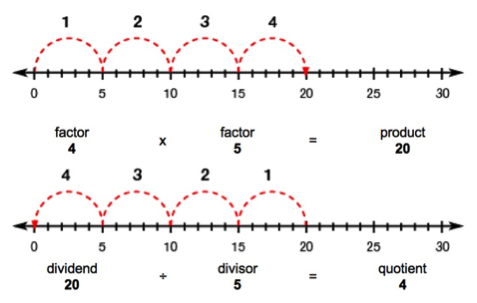
Image: Eduplace.com