What's the best way to learn grouping for adding and subtracting double and triple digit numbers?
There are so many different ways to teach adding and subtracting with two or three digit numbers. The idea of regrouping is very important for students to understand in order to feel comfortable either adding and/or subtracting larger numbers.
“Regrouping” is defined as the process of making groups of tens when adding or subtracting two digit numbers (or more) and is another name for carrying and borrowing.
When first introducing regrouping it’s best to use concrete manipulatives* and relate it to place value. The best manipulatives to use are base ten blocks. Base ten blocks help students “see” the value of each digit in the number and help to understand the “carrying or borrowing.”
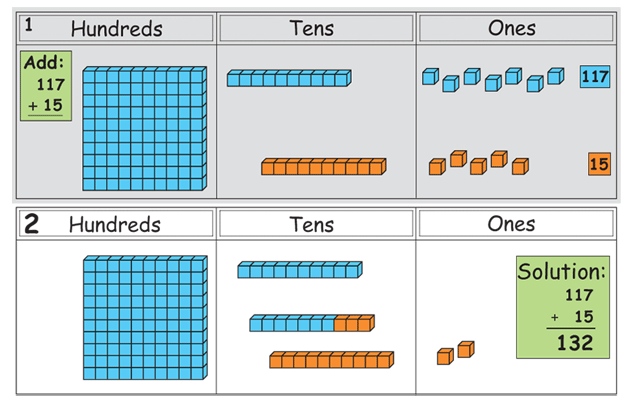
Image: www.inspiration.com
Once students have moved past the concrete stage, they can use pictorials to help them with regrouping. Many students prefer this “pictorial” phase because it’s easy for them to draw the blocks quickly and really understand if their answer makes sense.
Student’s work: The student can now see how many hundreds or “flats” (5 hundreds – 500), how many tens or “longs” (13 tens – 130, and so regroup those by circling 10 tens to make 100, with 3 tens – 30 left over) and how many ones (11 ones – 11, so regrouping by circling 10 ones to make 10, with 1 one – 1 left over).
So now: 600 + 40 + 1 = 641
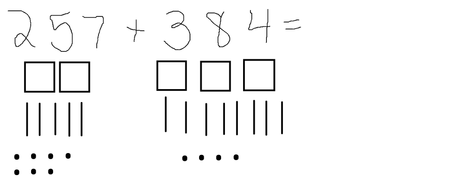
Image: www.showme.com/
The same can be done for subtracting:
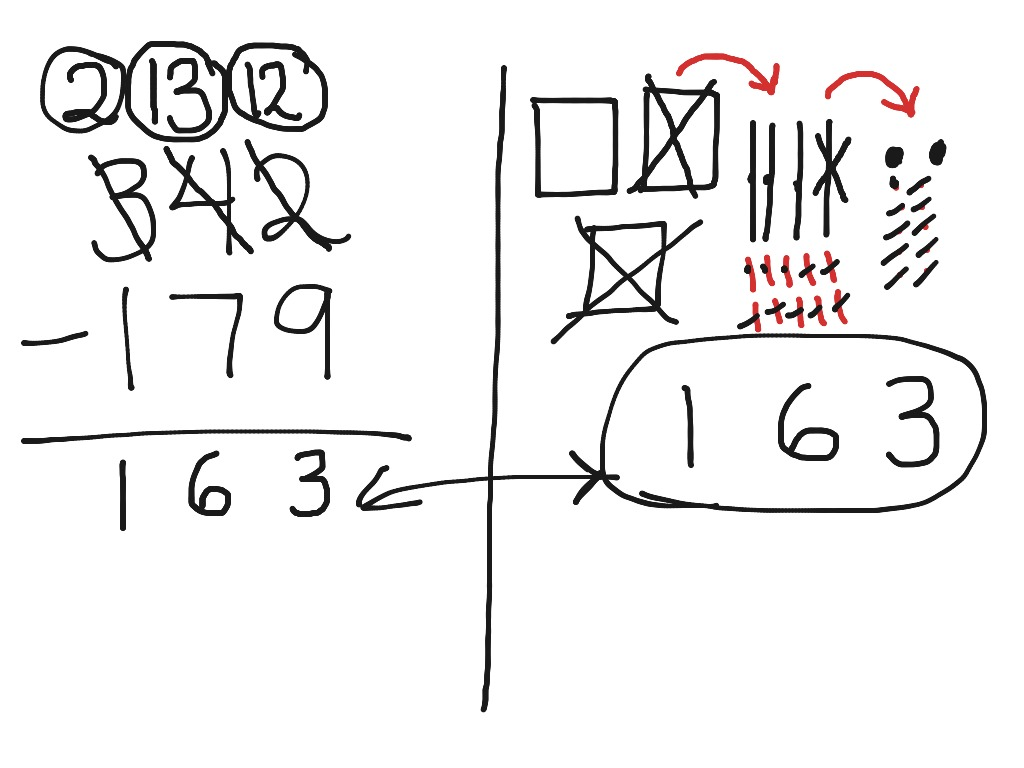
Image: www.showme.com
Another great way that doesn’t involve manipulatives or drawing models is using “split” addition or subtraction. Again, students can “see” the place value in each number and can understand the regrouping.
Split Addition:
647 --> 600 + 40 + 7
+ 285 --> 200 + 80 + 5
800 + 120 + 12 = 932
Split Subtraction:
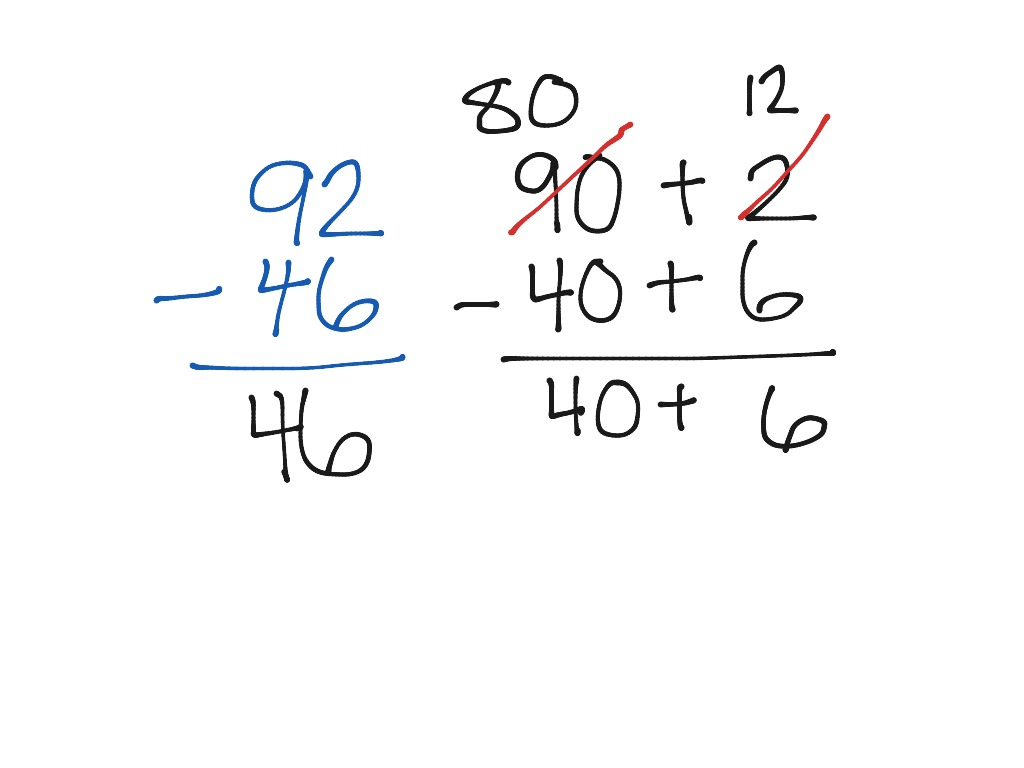
All of these strategies lead a child into computing the standard algorithm with ease. Of course whichever strategy a child chooses – the most important thing is they understand what they’re doing. We don’t want them memorizing steps without having any idea of what or why they’re doing those steps!