Preinstructional Planning
Objectives
Students will:
- Identify the properties of right triangles, i.e., that they have one right angle and two acute angles, and that the side opposite the right angle is called the hypotenuse
- Indicate that the formula for finding the length of the hypotenuse is a2 + b2 = c2, where a and b are the two triangle sides extending from the right angle and c is the hypotenuse
- Use the Pythagorean Theorem to find the distance between two points on a coordinate grid or the diagonal of a rectangle
Materials
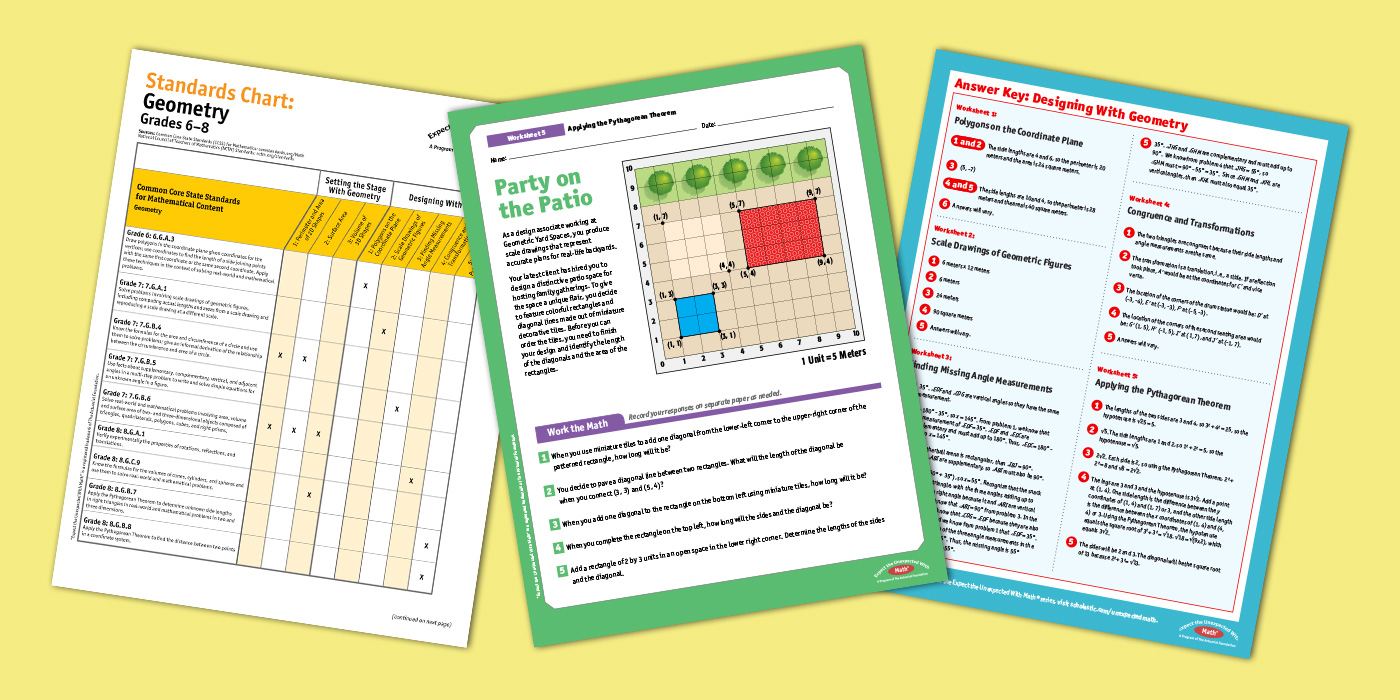
- Party on the Patio: Applying the Pythagorean Theorem printable
- Answer Key: Designing With Geometry printable
- Standards Chart: Geometry printable
- Graph Paper
- Scissors
- Whiteboard or large graph paper and markers
During Instruction
Set Up
1. Make a class set of the Party on the Patio: Applying the Pythagorean Theorem printable.
2. Print a copy of the Answer Key: Designing With Geometry printable for your use.
Lesson Directions
Introduction to Applying the Pythagorean Theorem
Step 1: Review the properties of right triangles as necessary for your class. Draw a right triangle on a grid on the board, using the right-angle symbol to identify the right angle, and labeling the hypotenuse C, one leg A, and the other B.
Step 2: It is a common misconception that the length of the hypotenuse equals the number of grid intervals it passes through. This can be demonstrated to be false by taking a square piece of paper, making a diagonal cut, and holding the hypotenuse of one of the right triangles formed by the cut next to one of the legs of the other right triangle.
Step 3: Show an example of the Pythagorean Theorem on the board, labeling one leg 3 meters, the other 4 meters, and the hypotenuse 5 meters. Indicate that the formula for side lengths in a right triangle is a2 + b2 = c2. Show how a2 + b2 = c2; in this case, 32 + 42 = 52. Repeat with another example, such as a right triangle with sides of 5 meters, 12 meters, and 13 meters, where 52 + 122 = 132.
Step 4: Indicate that the Pythagorean Theorem can be used to find the missing side length of a right triangle when the other two side lengths are known. For a triangle where one leg is 6 meters and the other is 8 meters, show how 62 + 82 = 100 and since √100 = 10, the length of the hypotenuse is 10 meters.
Step 5: Further demonstrate how the Pythagorean Theorem can be used to find the missing leg length of a right triangle when the lengths of the other leg and the hypotenuse are known. For example, in a right triangle where the one leg measures 9 meters and the hypotenuse measures 15 meters, write 92 + x2 = 152. So 81 + x2 = 225, which can be rewritten as x2 = 225 - 81. Thus, x2 = 144. Since √144 = 12, the length of the missing side is 12 meters.
Step 6: Finally, provide an example where the missing side isn't a whole number. For example, if both side A and side B measure 1 cm, then c2 = 12 + 12. Therefore, c2 = 2, so c = √2.
Step 7: To demonstrate how the Pythagorean Theorem can be used to find the length of the diagonal of a rectangle, draw a rectangle on a grid with the following coordinates: A (-2, 2), B (-2, 6), C (-5, 6), and D (-5, 2). Ask how the length of segments AC or BD could be found. Point out that the diagonal creates two right triangles, one of which is ΔABD.
The length of AD = 3 (subtracting the x-coordinates: -2 -5 = 3). The length of AB = 4 (subtracting the y coordinates: 6 - 2 = 4). Applying the Pythagorean Theorem, 32 + 42 = segment AD2. 9 + 16 = 25, so AD = √25 which is 5.
Step 8: To demonstrate how the Pythagorean Theorem can be used to find the distance between two points, draw points (3, 2) and (6, 6) on a grid. Ask the class how they can find the distance between the two points. Remind them that the distance is not equal to the number of grid intervals between the two points. Add a third point at (6, 2) and note that the three points form a right triangle when connected. Show how the horizontal leg is 3 units in length by subtracting the x-coordinates of the original two points.
Then show how the length of the vertical leg is 4 units by subtracting the y coordinates of the original two points. Using the Pythagorean Theorem, the distance between the two original points is 5 units (32 + 42 = 52, which is 25, and √25 = 5). Point out that instead of adding (6, 2) as the third coordinate, (3, 6) could also have been used to create the triangle. Point out that these two right triangles are congruent because they have the same side lengths and angle measurements.
Guided Practice
Step 9: Distribute graph paper to students. Write the following two points on a grid on the board: A (2, 10) and B (8, 2). Students should pair up and find the distance between the two points.
Answer: The distance = 10 units. Students should construct a right triangle by adding point C at (2, 2). [Note: (8, 10) would also work but this example uses (2, 2).] The distance of AC = 8, which is obtained by subtracting the two y-coordinates (10 - 2). The distance of BC = 6, which is obtained by subtracting the two x-coordinates (8 - 2). Using the Pythagorean Theorem, 82 + 62 = (segment AB)2. 64 + 36 = 100, which means that segment AB = √100 which equals 10.
Step 10: Checking for Understanding: Review answers as a class and respond to any questions.
Independent Practice
Step 11: Assign the Party on the Patio: Applying the Pythagorean Theorem printable for classwork or homework.
Step 12: Checking for Understanding: Review the answers to the Party on the Patio: Applying the Pythagorean Theorem printable, which are provided on page 1 of the Answer Key: Designing With Geometry printable. Make sure students explain their mathematical thinking. Address any misconceptions that may arise.
Post Instructional
Standards
- Grade 8: Pythagorean Theorem (CCSS: 8.G.7 & 8)
- Grades 6–8: Making Sense of Problems, Reasoning, Constructing an Argument, Using Appropriate Tools, and Attending to Precision (CCSS MP1–3 and 5–6); NCTM Geometry
For more information, download the comprehensive Standards Chart: Geometry printable.